What is Data Conversion in Programming?

Learning Goals

By the end of this tutorial, you should be able to:

Understand how Binary number work
Understand how Hexadecimal numbers work
Convert Decimal numbers to Binary number
Convert Decimal numbers to Hexadecimal number
Convert Hexadecimal numbers to Binary number
Understand the applications of data conversions

What is Data Conversion?

Data conversion is changing one format of receiving/storing data into another format. These formats are usually in decimal numbers, binary numbers, and or hexadecimal numbers.

Application Of Data Conversion/ Why Data Conversion Is Useful

Data conversion is used for reasons that not all specific files and formats can access and read all data types. As a solution data can be converted into different formats to allow a wider range of softwares to enter and use the data. This idea permits great flexibility and grants the user to use data as you’d like.

Understand What Binary is?

Binary numbers are numbers that are expressed in the digits ‘1’ and ‘0’. The number of 1’s and 0’s represent an increase to the original base 2⁰. Looking at the chart below the base of each binary position increases by a power of 1 from the previous, and all with a base of 2. The word binary means two which indicates why the base of each binary number is 2. Each binary position can only be used once or never, hence the reasoning behind ‘1’ and ‘0’. ‘1’ meaning the number is used and ‘0’ meaning the number is not used.

NOTE: The binary bases continue past 2⁷. You can continue increasing the power to be able to hold a larger decimal value!

128	64	32	16	8	4	2	1
2⁷	2⁶	2⁵	2⁴	2³	2²	2¹	2⁰

NOTE Can only be represented by a one or zero meaning a number can only be used once. You can add the corresponding decimal values together to receive the total decimal number.

Understand What Hexadecimal is?

Hexadecimal numbers are numbers that are expressed in the digits 0 to 9 and letter A to F. The numbers are representative of themselves and the values that we know they stand for. The letters on the other hand are assigned numbers, 10 to 15 in the order of A to F. Looking at the chart below we can see the side by side assigning of the decimal representation of each hexadecimal number. Hexadecimal numbers can be used over and over just like decimal numbers and unlike binary numbers. The word ‘hexa’ means six, and the word ‘decimal’ means ten. Ten and six together makes 16, which are the total number of digits in hexadecimal base values.

F	E	D	C	B	A	9	8	7	6	5	4	3	2	1	0
15	14	13	12	11	10	0	8	7	6	5	4	3	2	1	0

NOTE Each number or letter represents a decimal number. You can use each digit multiple times and you are to use add their corresponding decimal values to get the total decimal number.

Decimal to Binary:

Divide the number by 2
- The remainder is the binary number 0 or 1
- Next take the quotient and divide that by 2 as well and record its remainder
- Keep doing this till the quotient is 0
The remainders should be placed in order from the last remainder to the first to get your binary output

Decimal Number / 2	Quotient	Remainder
13/2	6	1
6/2	3	0
3/2	1	1
1/2	0	1
Therefore the binary equivilant of 13 is 1101.

Decimal to Hexadecimal:

Divide the number by 16
- The remainder is the binary number 0-F
- Next take the quotient and divide that by 16 as well and record its remainder
- Keep doing this till the quotient is 0
The remainders should be placed in order from the last remainder to the first to get your binary output

Decimal Number / 2	Quotient	Deciaml Remainder	Hexadecimal Remainder
7562/2	472	10	A
472/2	29	8	8
29/2	1	13	D
1/2	0	1	1
Therefore the Hexadecimal equivilant of 7562 is 1D8A.

Hexadecimal to Binary:

Convert the number back into decimal by simply adding.
- If binary add the base numbers 2^x (x being the base number)
- If hexadecimal add the numbers as usual and add the number which the letters represent.
Once the conversion is into decimal convert into the format of choice from the examples above.

Example Activity

In this example we will explore how different values in hexadecimal can display various colours on an RGB LED!!

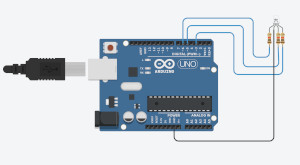
In the code we will need to initialize a pin for each leg of the LED. Now to be able to change and see the different colour you can make, edit the values in analogWrite(red,0x79); , analogWrite(green,0x2A); , and analogWrite(blue,0xDB); . Keep the 0x as that indicates that the input is in hexadecimal. The limitations range from 00 to FF, so you have quite the range to explore with different values.

const int red = 6;  // name the output pins controlling the RGB
const int blue = 5;
const int green = 3;

void setup()
{
  pinMode (red, OUTPUT);
  pinMode (blue, OUTPUT);
  pinMode (green, OUTPUT);
}

void loop()
{
  //write the pin with the hexadecimal value

  // HERE!!! change the values for all three of these lines of 
  // code can see how the colour changes with different values!!
  analogWrite(red,0x17);
  analogWrite(green,0x4D);
  analogWrite(blue,0xEA);

}

Your Turn!

Try creating a program that uses 4 LED's to count in binary from 0 - 15!

Pratice taking decimal numbers and converting them into binary values
To make it harder create this program but with RGB LED's and ask a user for input of what colour the LED's should count in binary with

Free spirit!! Try messing around with the program above and see how many cool colours you can create using Hexadecimal numbers.